- Вы можете скачать этот материал в PDF (~450 кБ)
Теорема о биссектрисе сформулирована еще в шестой книге «Начал Евклида» (300 лет до н.э.).
Формулировка: Биссектриса треугольника делит противоположную сторону треугольника на два отрезка, длины которых пропорциональны соответствующим прилежащим сторонам треугольника.
Существует несколько вариантов доказательства. Как правило это:
- Метод площадей;
- Приведение дополнительными построениями к подобным треугольникам.
Покажем оба метода и рассмотрим, как можно упростить метод площадей.
Начнем с метода площадей. Он, к сожалению, использует тригонометрическую функцию sin. (Формула S=a·b·sinα/2 дается неоправданно поздно, где-то 9-й кл.). C формулой S=a·h/2 начинают знакомить еще в 5-м. С биссектрисой знакомят в начале 7-го класса. С подобными треугольниками – в начале 8-го.
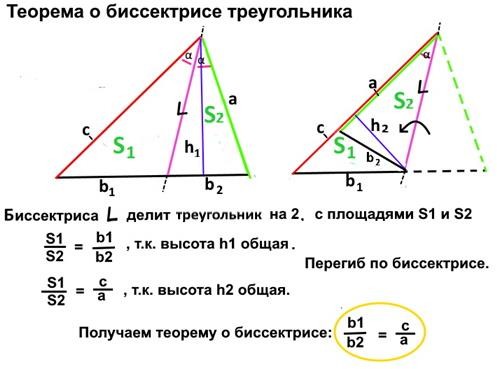
Метод площадей (рисунок ниже).
Рассматривается отношение площадей двух треугольников, создаваемых биссектрисой. Сначала их площади вычисляются по соответствующей боковой стороне, биссектрисе и синусу угла α между ними.
Потом то же отношение площадей вычисляется через высоту и основания обоих треугольников. Приравнивая, получаем соотношение теоремы биссектрисы.

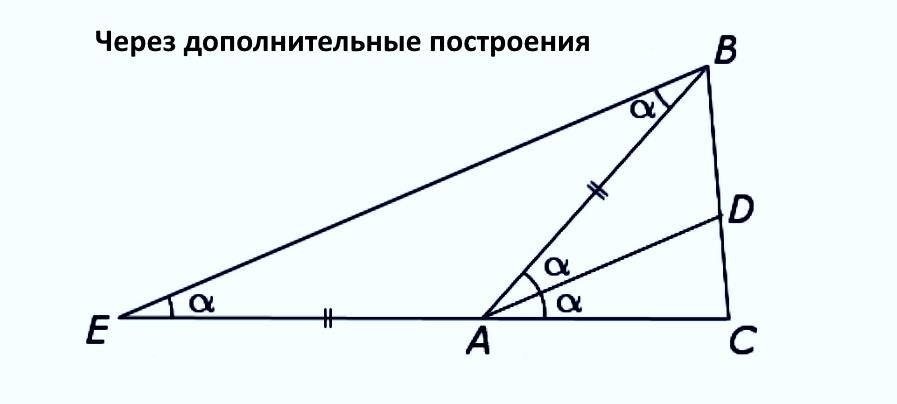
Теперь рассмотрим два способа, использующих дополнительные построения к треугольнику ABC, сводящие задачу к соотношению подобных треугольников (тема 8-го кл.).
Первый метод.
Из одной боковой вершины (B) треугольника ABC строится прямая, параллельная биссектрисе. Получаем 2 подобных треугольника. В основании имеем отношение боковых сторон исходного треугольника. На другой стороне
(справа) имеем два отрезка, на которые биссектриса делит сторону BC. Ясно, что оба отношения одинаковы. Построение и далее доказательство не самые простые.
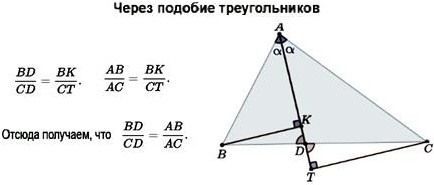
Второй метод.
Из боковых вершин строятся 2 перпендикуляра к биссектрисе. Сначала рассматривается отношение малых треугольников при основании BKD и CTD, которые пропорциональны двум частям основания. Затем смотрят отношение прямоугольных треугольников ABK и ACT. У них то же отношение, что и у малых треугольников.
А вот предлагаемый вариант метода площадей, но без использования функции sin. Его можно давать сразу с изучением биссектрисы. С 7-го класса.
Учителю, если предоставляется возможность, нужно давать ученикам простые доказательства в качестве пропедевтики. «Сеять зерна». Наши учебники и подходы страдают обязательным пирамидальным построением: ничего о том, что в пирамиде по программе стоит одним или двумя этажами выше. «Не положено!»
Но дети не роботы. Они этой «железной пирамидальности» общей картины не воспринимают! Может быть, потом, в зрелом возрасте. А в своем возрасте они строят мир из фрагментов. А такие моменты пропедевтики делают уроки интереснее. Отрицание пропедевтики – это наша традиционная неадекватность.