Этот учебник вы можете скачать в PDF (~ 2,5 Мб)

Посвящается ученику Олегу Федотову

Ученики не любят объемных текстов. Но учителя вынуждены придерживаться выбранного учебника. Большой объем материала приводит к тому, что программа «проходится». Без отработки и повторов. А ведь «повторение – мать учения».

Из-за объемности текста материал плохо структурируется в сознании учеников.

В данном изложении текст первоисточника сокращен до 30 страниц, но практически без потери содержательных моментов. Акцент делается на существе тем. Сопровождающие картинки в определенном смысле являются «опорными сигналами» и позволяют ученикам быстро вспоминать содержание прошлого материала.

Предполагается, что на уроке должно хватать времени на повторение пройденного.

(18) Сила выталкивания Архимеда. Доказательство Архимеда. Физическое объяснение. Плавание тел на поверхности. Воздухоплавание. Интересные опыты. Давление в жизни. Гидравлический пресс.

(21) Работа, мощность и энергия. Работа. Энергия, потенциальная и кинетическая. Мощность. Гидростанция. КПД. Ветряные двигатели.

(25) Простые механизмы. Рычаги, наклонная плоскость, блоки. Разные виды рычагов.

(27) Момент силы.

(27) Центр тяжести. Устойчивость. Равновесие тел, имеющих площадь опоры. Другой подход к проблеме устойчивости.

§ 1. Что изучает физика

Аристотель. 4-й век до н.э. Грек из знатного рода.

Слово «физика» происходит от греческого слова «фюзис», что означает «природа», идет от названия трактата Аристотеля из 8 книг.

Там впервые были определены такие понятия: пустого пространства, места в этом пространстве и времени.

Но много там и «умозрительных» выводов, без реального обоснования.

Например, то, что тяжелые тела падают быстрее. Это позже опроверг Галилей.

Или то, что «природа не терпит пустоты». Это утверждение опроверг ученик Галилея Торричелли, когда Галилей поручил ему разобраться, почему рабочим не удавалось поднять по трубе воду выше 10 метров, откачивая воздух.

Итак, физика работает с природой, ее явлениями.

Изучением природы занимаются и другие науки: биология, химия, астрономия.

Но все они строятся на фундаменте общих законов физики.

§ 2. Понятия физики: физическое тело, вещество, материя.

Вещества – это то, из чего состоят тела, например, соль, медь.
А вот невещественные понятия: свет, звук.
Понятие «материя» требует особых пояснений. Материей называется то, что существует независимо от нашего сознания (наши сны нематериальны).

§ 3. Этапы построения знаний: наблюдения, эксперименты, поиск закономерностей, попытки объяснить их (гипотезы).

Если гипотезы подтверждаются – они становятся теориями.

§ 4. Физические величины и их измерение.

Многие физические явления характеризуются величинами. Для оценки величин требуются меры, некоторые условные единицы.

Например, раньше это были аршин, пуд. Сейчас, например, электрический ток измеряется в амперах.

«1 ампер» – специальная единица. Предположим, ваш прибор амперметр показывает «4 А». Это значение вам указывает стрелка на шкале амперметра или цифры на дисплее.

С 1963 года в России и других странах принята система мер СИ (система интернациональная). В ней основными мерами являются: единица длины метр (1 м), единица времени секунда (1 с) и единица массы килограмм (1 кг). Все остальные (не основные) меры можно выразить через основные меры.

Раньше пользовались другими системами (не СИ), и в некоторых научных областях ими пользуются и сейчас.

Эталоны хранятся в Палате мер. Но сейчас используется только эталон массы. Для сохранения мер длины и времени используют другие специальные методы.

Меры можно использовать с десятичными коэффициентами. Для этого используются некоторые приставки: мега (1000 000), кило (1000), гекто (100), дека (10). Или уменьшающие: деци (0.1), санти (0.01), милли (0.001), микро (0.000 001).

Например, километр, дециметр, сантиметр, миллиметр, микрон, и т.д.

§ 5. Точность и погрешность измерений.

На показанном амперметре значение указывается стрелкой. Для таких приборов важное понятие – цена деления.

На рисунке видно, что между отметками «0.5» и «1» 10 делений. Значит, цена одного деления (1- 0.5)/10 = 0.05 А.

У приборов есть такое понятие как погрешность. Она бывает абсолютной, т.е. прямо дается ее значение. Например, ±0.02 А, независимо от положения стрелки.

Но бывает, что ошибка измерения пропорциональна самой величине. В этом случае погрешность называется относительной и дается в процентах от измеряемой величины. Например, если дана погрешность 1 %, а прибор показывает 1.5 А, то ошибка будет ±1.5 ·0.01 А=±0.015 А.

Старинные меры

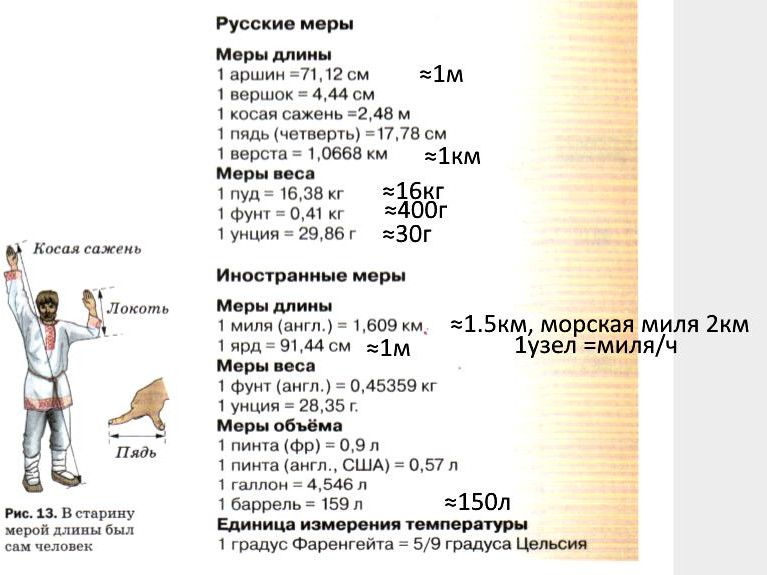
Отработайте внимательно и постарайтесь запомнить только отмеченные меры. Знание их поможет вам читать художественную литературу.

Сейчас в России применяется Международная система единиц.

§ 7. Внутреннее строение из частиц. Обоснования.

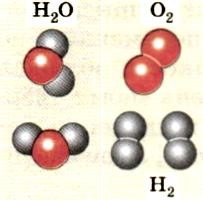Все вещества состоят из атомов. На рисунке они изображены шариками.

Изображены молекулы (т.е. простые структуры из атомов): молекула воды (H2О, 2 атома водорода и 1 атом кислорода), молекула кислорода (O2, 2 атома кислорода) и 2 молекулы водорода (H2, 2 атома водорода).

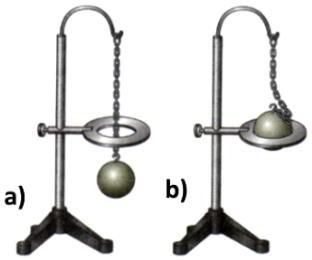
§ 8. Расширение тел и веществ – одно из доказательств молекулярного строения вещества.

Слева: холодное ядро проходит в отверстие, а нагретое – нет.

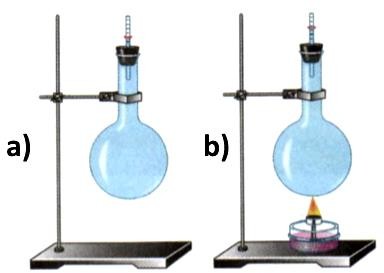Ниже: Если колбу, заполненную водой, закрыть пробкой с трубкой (специально тонкой для повышения точности), то при нагревании колбы видно, что уровень воды в трубке поднимается.

§ 9. Броуновское движение

Броуновское движение является еще одним доказательством молекулярного строение веществ.

В 1827 году британский ботаник Роберт Броун, купив хороший микроскоп, решил посмотреть на очень мелкие споры растений в воде. Он с удивлением увидел хаотичное движение спор. Это могло быть объяснено только хаотичным движением более мелких, невидимых в микроскоп частиц, т.е. молекул воды.

§ 10. Явление диффузии

Диффузия – это взаимное проникновение атомов или молекул одного вещества в другое.

Слева показана диффузия жидких веществ. В мензурку наливают раствор медного купороса, имеющего ярко-голубой цвет. Затем осторожно доливают воды. Через несколько дней видно взаимопроникновение молекул купороса и воды.

Интересно, что диффузия имеет место и между твердыми телами. Например, если взять хорошо отшлифованные пластинки свинца и золота и плотно сжать их, то через 4 года вы увидите явное взаимное проникновение.

§ 11. Разное взаимодействие молекул разных веществ

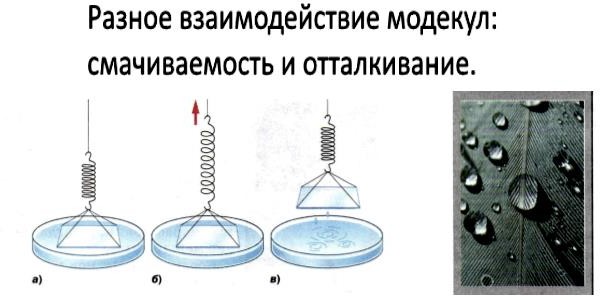Молекулы разных веществ взаимодействуют по-разному. Это хорошо видно на явлении смачиваемости. На левом из рисунков показано, как атомы металлической пластинки «прилипают» к поверхности воды, так, что оторвать пластину можно только с усилием. Эта поверхность «смачивается».

На правом из рисунков видно, как капельки воды отталкивается от поверхности, она (не смачивается).

§ 12. Три агрегатных состояния вещества

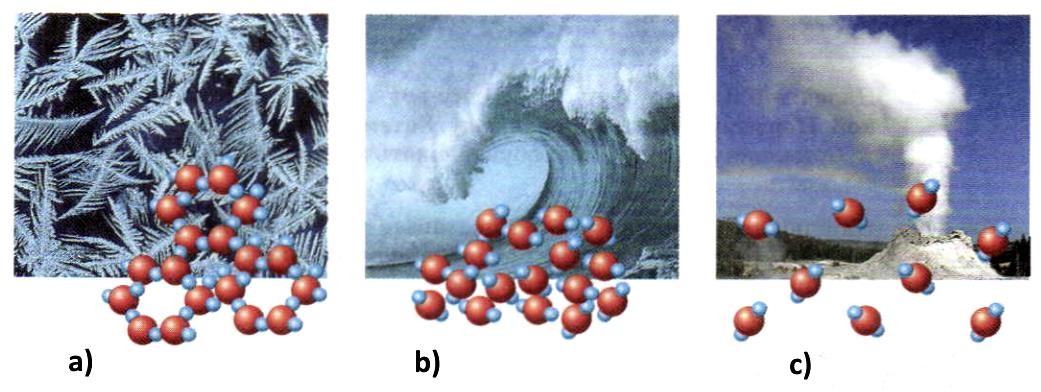
Одно и то же вещество может быть в разных агрегатных состояниях. Мы будем знакомиться с тремя агрегатными состояниями: твердым, жидким и газообразным.

Например, вода. В твердом состоянии она лед, в жидком – собственно вода, в газообразном – пар.

В твердом состоянии (a), лед, молекулы воды образуют соединения (кристаллы) с жесткой структурой. Почему она жесткая именно при низкой температуре? При низкой температуре двигательная энергия молекул (т.е. их колебаний) снижена. Поэтому связи между молекулами крепкие, структура жесткая.

В жидком состоянии (b) температура выше, значит, энергия движения больше.

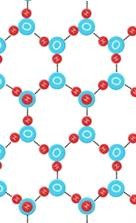Отойти друг от друга молекулы не могут, но могут изменять свои взаимные положения. Поэтому жидкость легко меняет форму, заполняя объемы разных форм. Но поскольку молекулы близки друг к другу, жидкость практически несжимаема.

В газообразном состоянии (c), пар. При более высокой температуре молекулы отделены друг от друга, они свободно движутся в пространстве, газ (пар) сжимаем.

То, что одно и то же вещество может быть в разных состояниях лишний раз

доказывает молекулярное строение веществ.

Из-за жесткой структуры молекулы льда «упакованы» менее плотно, чем у воды.

§ 14. Время

Единицы: секунда (с), минута (мин)=60 с, час (ч) =60 мин =3600 с.

Сутки=24 ч, месяц (мес.)=30-31 суток (в феврале 28 или 29), время обращения Луны вокруг Земли ≈30 суток, «месяц»), год (г)=12 мес.≈365 суток (время обращения Земли вокруг Солнца).

Приборы: часы, секундомер.

Длительность секунды примерно равна времени произнесения «двадцать один». Считают: «двадцать один, двадцать два, двадцать три…».

§ 15. Длина

Единицы длины: метр (м), километр (км), дециметр (дм), сантиметр (см), миллиметр (мм), микрометр (мкм). Микрон (мк) – то же, что микрометр.

Примеры: 1 км – прибл. расстояние между остановками городского транспорта,

100 м – длина футбольного поля.

600 км – расстояние от Москвы до Петербурга,

6300 км – радиус Земли,

40 000 км – длина экватора Земли,

40 000 км – высота геостационарной орбиты, по которой спутники летят совместно с поворотом Земли, и они как бы «висят» над одним местом Земли.

400 000 км расстояние до Луны,

150 000 000 км расстояние до Солнца.

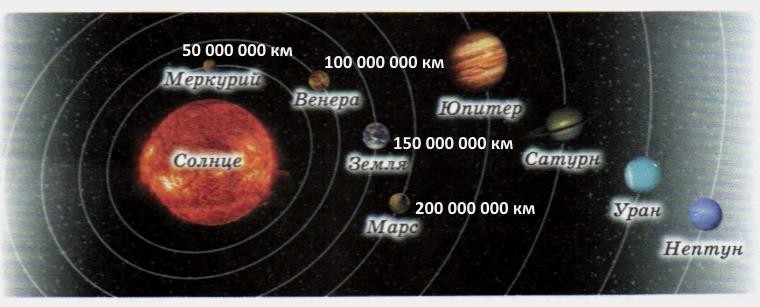
§ 16. Скорость

Запомните приближенные расстояния до ближних к Солнцу планет. Это не сложно. Они идут примерно через 50 000 000 км.

Меркурий похож на Луну. Венера похожа размерами на

Землю, но температура там 300°C.

Марс – пустынная планета, практически без атмосферы, но есть признаки воды в виде льда.

S делим не «на» v, а «по» v (сколько раз v укладывается на S). Путь S можно рассматривать в координатах t и v как площадь прямоугольника под линией v(t).

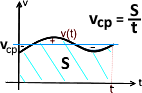При равномерном движении v =S/t. (деление «на») При неравномерном движении vсредняя=S/t.

На графике справа S – это площадь под кривой v(t), а vср – уровень прямой

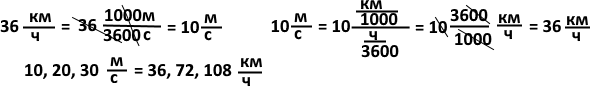Единицы скорости: м/c, км/ч, км/c. Примеры перевода единиц:

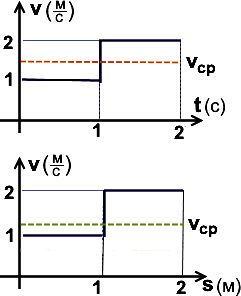Частая ошибка при вычислении средней скорости

vср= (суммарный путь)/(суммарное время). На верхнем графике v(t), а на нижнем v(s).

На верхнем графике (v от t) суммарный путь: s1+s2=v1·t1+v2·t2=1·1+2·1=3 м. Суммарное время: t1+t2=1+1=2 с. vср= (суммарн. путь)/(суммарн. время) =3/2=1.5 м/с.

На нижнем (v от s) сложнее. Суммарный путь: s1+s2=1+1=2 м.

Суммарное время = t1+t2 = S1/v1+ S2/v2 =1/1+1/2 =3/2 с .

vср= (суммарн. путь)/(суммарн. время) = 2/(3/2) =4/3 = 1.33 м/с. Осторожнее с v(s)!

§ 17. Примеры скоростей:

Скорость пешехода – 5-6 км/ч, скорость бегуна (рекорд) 10 м/с,

скорость пассажирского самолета 800 км/ч, при посадке 300 км/ч, скорость пули – 800 м/с ≈ 1 км/с,

я космическая скорость ≈ 8 км/c, это скорость низколетящего спутника,
я космическая скорость ≈ 11 км/с, достаточна, чтобы выйти из поля Земли, скорость движения Луны вокруг Земли 1 км/с,

скорость движения Земли вокруг Солнца 30 км/с, скорость звука в воздухе 340 м/с или 1000 км/ч

Число Маха – скорость сверхзвуковых самолетов, выраженная в скоростях звука. Например, скорость 2 М обозначает скорость 2 х 340 м/с или 2 х 1000 км/ч.

Скорость звука в воде 1500 м/с.

Скорость света 300 000 км/с, от Земли до Луны свет идет немного более 1 с, от Солнца до Земли свет идет 8 мин. По экватору световой луч (радиоволна) проходит более 10 раз за секунду.

Скорость в разных системах

2 системы: Sys1 (покоящаяся) и Sys2 (движущаяся). Как скорость мяча, брошенного в Sys1 со скоростью v1, будет восприниматься из Sys2 (v2)? Скорость транспорта V.

На двух рисунках отражено 2 случая: транспорт движется от мяча, и против мяча.

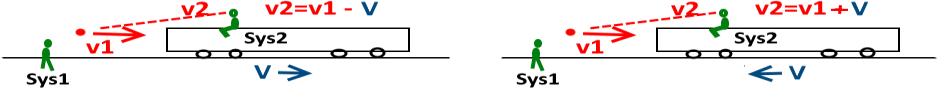
1-й космическая скорость (скорость низколетящего спутника по круговой

орбите).

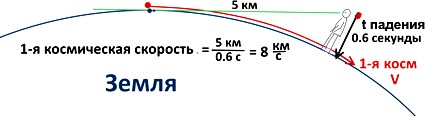
Известно, что человек среднего роста (1.75 м) видит линию горизонта на расстоянии 5 км.

И известно, что тело падает с высоты 1.75 м за 0.6 с.

Тело за 0.6 с должно пролететь 5 км за то же время, что оно падает с высоты 1.75 м, чтобы оказаться на том же расстоянии от поверхности Земли, что и было. 1-я космическая V = 5 км/0.6 с = 8 км/c.

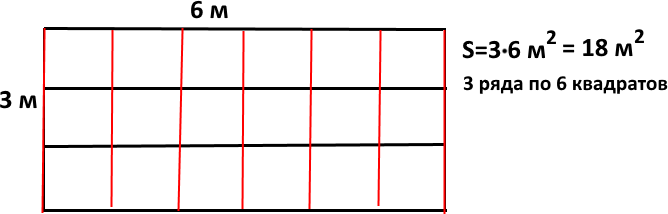Площадь S = n·m

1 м2 =100 дм2 (10 дм·10 дм) =10 000 см2 (100·100)

Единицы площади:

1 км2 = 1000 м x 1000 м= 106 м2,

1 га (гектар) = 100 м x 100 м = 104 м2, примерно площадь футбольного поря. 1 а (ар) = 10 м x 10 м = 100 м2 или 1 сотка, небольшой участок – 6 соток.

1 см2 = (1/100) м x (1/100) м =10-4 м2

Объем

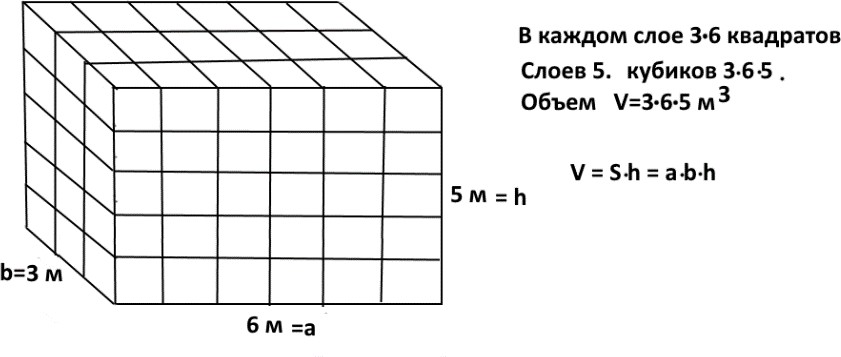1 км3 = 1000м x 1000м x 1000м = 109 м3 .

1 м3 = 1000 дм3 (10 дм ·10 дм ·10 дм) 1 м3 = 106 см3 = 109 мм3

1 дм3 = 1 литр Стандартное ведро – 10 л

Масса

Определение: Масса – характеристика инерции тела.

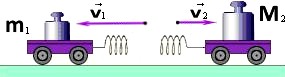При отталкивании тел друг от друга скорости тел обратно пропорциональны их массам.

1 т (тонна) = 1000 кг

1 г (грамм) = 10 -3 кг

1 мг = 10 -3 г Единица массы 1 кг.

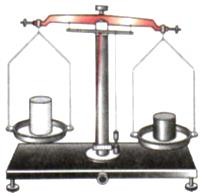Сравнивать массы можно и на весах, так как тела притягиваются Землей пропорционально их массам. На

«рычажных» весах (слева) можно сравнивать массы и на Луне. Но пружинные весы на Луне покажут результат в 6 раз меньше, чем на Земле из-за меньшей силы притяжения там.

1-й способ (отталкивание масс друг от друга) работает в любых ситуациях, в том числе и на космическом корабле в условиях невесомости, где использование весов бесполезно.

Плотность

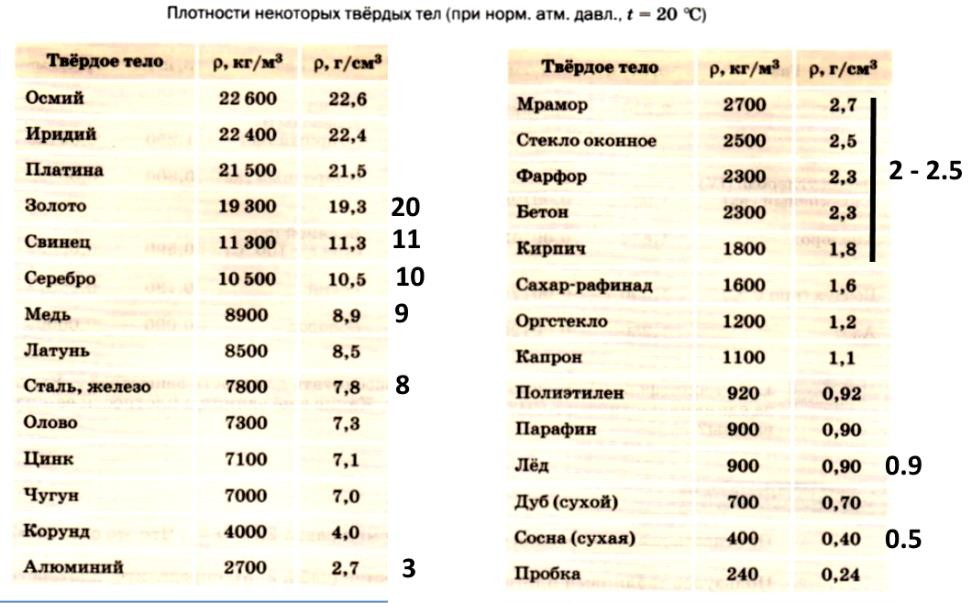Определение: Плотность вещества – это его масса на единицу объема.

Как правило, обозначается буквой

𝝆. Размерность: кг/м3, т/м3 , или кг/дм3, или г/см3 . 𝝆=m/v.

Какова 𝝆 золота пробы 500 ? Это 50 % золота (по массе) и 50% серебра.

Возьмем mзолота = mсеребра =1 г .

𝝆 золота = 20 г/см3 , 𝝆 серебра =10 г/см3 -> vзол = 1г/20 г/см3 , vсер = 1г/10 г/см3 , m=2 г, v= (1/20 + 1/10) см3 = 3/20 см3 .

𝝆 =2г/(3/20 см3) =40/3 =13.33 г/см3 Отметьте, что 𝝆 ближе к 𝝆серебра=(10 г/см3).

Плотность воздуха 1.3 кг/м3, это примерно в 1000 раз меньше плотности воды. Масса кубометра воды – 1000 кг = 1 т.

Пример: Найти 𝝆 смеси: 1 литра воды и 2 литров серной кислоты. Вода vводы 1 л mводы = 1 кг.

Кислота vкисл 2 л mкисл = 2 л х 2 кг/л = 4 кг.

𝝆смеси = m/v = (1+4)/(1+2) кг/дм3 = 5/3 кг/дм3 = 1.66 кг/дм3

Ускорение. Равноускоренное движение

Определение: ускорение — изменение скорости за единицу времени.

Например: скорость изменяется на 3 м/c за 1 секунду, a=3 м/с2, читается «3 метра в секунду за секунду». Если со знаком «–», то это «замедление» (уменьшение скорости).

Стандартно обозначается буквой «a». Если речь идет об «ускорении свободного падения», то оно обозначается «g», g≈10 м/с2, ( точнее, 9.81 м/с2 ),

Если начальная скорость нулевая (v0=0), то v(t)=a·t (=g·t в случае падения).

Рассмотрим падение камешка с высокого балкона (v0=0). v(t)= g·t. Вычислим длину пути падения за первые 3 с. Конечная скорость v(3)= g·t=10·3 =30 м/с.

Средняя скорость: vср= (0+g·t)/2=g·t/2. В нашем случае: vср=(0+30)/2=15 м/с. Пройденный путь: s= vср·t= (g·t/2) ·t = g·t2/2. В нашем случае: s=15 м/с ·3 с=45 м.

Если задана конечная скорость v (а не t), то удобнее использовать формулу:

s=v2/(2a). Как она получается? Средняя скорость vср =(0+v)/2=v/2. t=v/a. Получаем s= vср·t= v/2 · v/a = v2/(2a).

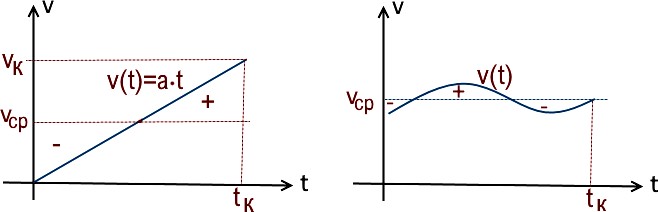По ускоренному движению от нулевой скорости (v0=0) нужны только 3 формулы:

v(t)= a·t , s= a·t2/2 или s=v2/(2a).

й график равноускоренного движения v(t) =a·t , vср =vк/2 , s= vср ·tк
й график с произвольно изменяющейся скоростью, s= vср ·tк , но средняя скорость

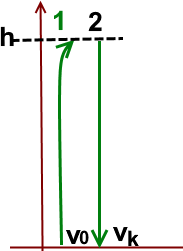vср выбирается так, чтобы площади над прямой (+) и под прямой (-) были равны.

На рисунке изображено движение вверх (1) с замедлением (a= – g) с начальной скоростью v0 до скорости 0. И движение вниз (падение) с начальной скоростью 0.

Если в движении 1 (подъеме) ход время изменить на противоположный, то получится движение 2.

Поэтому для вычисления s для 1 можно пользоваться формулами для 2: s= g·t2/2 и s=v2/(2g).

Вычислим время падения с высоты h=1.75 м (рост человека). Нами оно использовалось для вычисления 1-й космической скорости. h=1.75м = g·t2/2

t2 =(1.75· 2)/10= 0.35. t=0.6 с

Силы

Определение: сила – степень воздействия на тело.

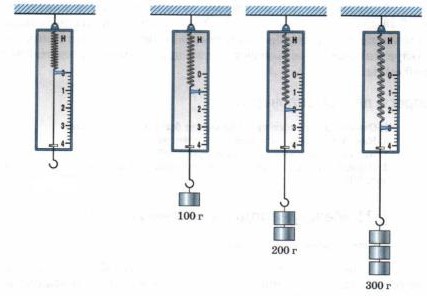
Единица: 1 Н (ньютон). Измеряется по степени растяжения или сжатия пружины динамометра. Пружина динамометра растягивается или сжимается согласно закону Гука: F=k·x, F-сила, x-растяжение, k-коэффициент

упругости пружины для конкретной пружины. При сжатии пружины x<0.

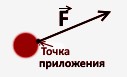Сила – это вектор, имеющий 3 характеристики: точку приложения, направление и величину. Обозначается стрелкой. Над буквой, обозначающей вектор, как правило, ставят стрелку или черточку: 𝐀⃗ или 𝐁̅.

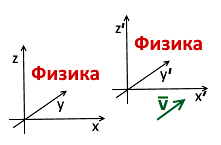
Инерциальная система: Это система, движущаяся в одном направлении с постоянной скоростью, без вращения.

Как пример: система, привязанная к железной дороге (земля), и равномерно движущийся вагон –это примеры инерциальных систем.

Принцип относительности: Любая инерциальная система равноправна для всех физических законов (нет выделенных систем). (В закрытом бесшумном вагоне, который стоит или который движется

равномерно, никак нельзя понять, стоит он или движется, вся физика в них одинакова. )

Законы Ньютона.

Законы, действующие в инерциальных системах Исаак Ньютон, выдающийся британский физик.

й закон Ньютона: Без действия силы на тело оно либо покоится, либо движется в одном направлении и с постоянной скоростью.
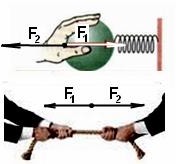й закон Ньютона: Под действием силы тело движется ускоренно: 𝐅 =𝐚⃗ ·m. 3-й закон Ньютона: Действие и противодействие равны и противоположны.

Замечание 1: Системы на поверхности Земли не является в точном смысле инерциальными, поскольку поверхность Земли не плоская, и сама Земля движется по круговой орбите. Но для наших задач эти системы могут считаться инерциальными,

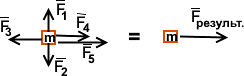Замечание 2: 2-й закон Ньютона F=am надо понимать более широко, для нескольких сил. Под силой F надо понимать векторную сумму всех внешних сил, действующих на тело. Эта сумма сил нарывается «результирующей силой».

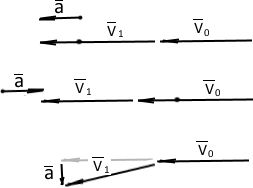Пока сила не действует на тело – оно движется по инерции в одном направлении и с одной скоростью. Воздействие силы вызывает измнение скорости тела и траектории.

Если F направлена в сторону движения тела (𝐕⃗ ), то ускорение (𝐚⃗ ) направлено в сторону движения тела (𝐕⃗ ), V увеличивается по величине. Если F направлена против движения – V уменьшается по величине.

Если F перпендикулярна движению – V изменяет направление, но величина V сохраняется.

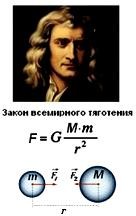Закон всемирного тяготения

G – гравитационная постоянная (коэффициент). M и m –массы.

Если r увеличить в 2 раза (в знаменателе r2), то сила F уменьшится в 4 раза. Т.е. на высоте 6300 км (еще один радиус Земли) вес тела P (и g) меньше в 4 раза.

Принцип движения вокруг Земли состоит в том, что тело движется вдоль поверхности и одновременно падает к центру с ускорением g. Но из-за кривизны поверхности Земли оно оказывается на том же расстоянии r от центра. Интересно, что объяснил это Ньютону физик Гук, его старший коллега.

Ньютон, будучи хорошим математиком, применил математику для точного

определения орбит движения планет. Мы так считали 1-ю космическую скорость.

Сила тяжести

Великий итальянский физик, сбрасывая одновременно пулю и ядро с пизанской башни (г. Пиза), показал, что все тела независимо от массы падают одинаково. До этого считалось, что тела с большей массой падают быстрей.

Он же показал, что все тела падают с одинаковым ускорением. Близко к поверхности Земли все тела падают с ускорение g≈9.81 м/c2 ≈ 10 м/c2.

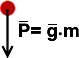Все массы притягиваются к Земле (вес тела). Как определяется эта сила? По 2-му закону Ньютона 𝐅 =𝒂⃗ m. А 𝒂⃗ =𝐠⃗ . Силу тяжести принято обозначать буквой P: 𝐏⃗ =𝐠⃗ m. Стандартно вектор силы тяжести приложен к центру массы.

Пример: m=2 кг. P =2 кг·10 м/c2 = 20 Н.

Иногда силу P НАГЛЯДНЕЕ давать не «20 Н.», а «вес массы 2 кг», «2 кг веса».

Почему всё-таки перышко и камешек падают по-разному? Из-за

сопротивления воздуха, которое на движение перышка сказывается больше.

Через 100 лет после опытов Галилея Ньютон показал это экспериментально. В одной пробирке с воздухом пуля, камешек и перышко падали по-разному (из-за сопротивления воздуха). В пробирке, из которой воздух был откачан – все предметы падали одинаково, с одинаковым ускорением g.

Сила реакции

Рассмотрим пример: человек стоит на Земле. Условно, покоится, т.е. Fрезульт.=0. На него со стороны Земли действует сила притяжения P=mg. Можно считать, что она приложена к центру человека. Значит, есть еще сила равная и противоположная P.

Рассмотрим силы, действующие на человека. На него действует две противоположные силы: P (вниз) и т.н. сила реакции N вверх со стороны Земли. Она возникает ровно такая, чтобы уравновесить силу P, не дать телу двигаться вниз. Ни больше, ни меньше. Поэтому она называется «силой реакции». Но это не пара сил из 3-го закона Ньютона!

А силы D (сила давления человека на Землю) и N (сила реакции Земли) образуют пару «действие-противодействие» по 3-му закону Ньютона в точке A.

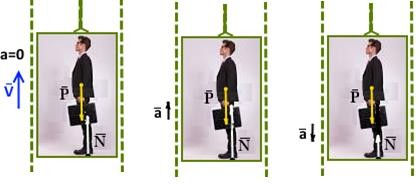На левом рисунке рассмотрен лифт в покое (v=0) или движении с постоянной скоростью v. Fрезульт.=0.

Значит, по величине P=N.

Чтобы человек (вместе с кабина лифта) получали ускорение вверх, (вес P неизменен) сила реакции пола должна быть: N> P -> N – P= amчел.

При ускорении вниз сила N должна стать меньше

P на ma: P-N= amчел. (ускорение a направлено вниз, mчел -масса человека).

Скоростной лифт несколько секунд может двигаться вниз с ускорением свободного падения g. В этом случае результирующая сила равна P=mчел·g, т.е. сила N должна быть равна 0. В кабине лифта будет в это время состояние невесомости. Как на космическом корабле.

Сила трения

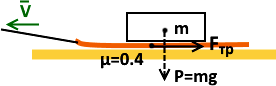Сила трения скольжения. На деревянной (легкой) доске установлен груз массой m. Доску с грузом тянут с помощью веревки по деревянному полу. Положим, m=1 кг.

Здесь сила сопротивления возникает из-за трения

дерева по дереву. От чего зависит эта сила сопротивления Fтр? В данном случае она называется силой трением скольжения.

Оказывается, Fтр скольжения зависит от двух моментов: 1)от пары трущихся материалов (в данном случае это дерево по дереву); 2)от силы прижатия этих

поверхностей друг к другу. Чем сильнее сдавливаются поверхности–тем труднее

тянуть.

Сила прижатия (в данном простейшем случае!) – это вес массы m: P=mg=10 Н.

Пара трущихся материалов определяет коэффициент трения μ<1, который показывает, какую часть Fтр составляет от силы прижатия. В данном случае дерева по дереву μ=0.4. Т.е. Fтр по величине равна 0.4 от силы прижатия (P=10 Н), т.е. Fтр = μ·P = 0.4 ·10 Н = 4 Н. И эта Fтр не зависит от скорости v, с которой доску тянут. (Важно, что она движется, не стоит на месте!) Таково трение скольжения!

Приблизительные значения μ: камень-камень 0.5, дерево-камень 0.5, дерево-дерево 0.4, дерево-металл 0.2, металл-металл 0.1, металл-лед (коньки) 0.01.

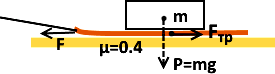Сила трения покоя. А что, если в предыдущем случае приложена сила F <4 Н, скажем, только 3 Н? Движения не будет. А сила сопротивления? Fтр теперь не 4 Н, а 3 Н! Почему? Т.к. тело не движется (ускорение=0), то по 2-му закону Ньютона сумма сил, действующих на доску, должна быть равна 0.

Силе трения Fтр в этом случае достаточно быть равной силе F, приложенной к доске, чтобы просто удерживать тело в покое. В данном случае Fтр является силой реакции, т.е. она проявляется ровно настолько, чтобы удерживать тело на месте. Но она не может быть больше μ·P.

Если для силы трения скольжения Fтр есть только одно значением = μ·P, то сила трения покоя может быть от 0 до μ·P, здесь μ·P определяется как предельное возможное значение силы сопротивления покоя: Fтр.предельное = μ·P. P-это Fприжатия.

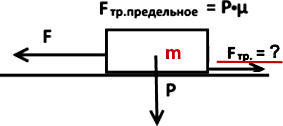Задача: К деревянному бруску массы m=2 кг на горизонтальной деревянной поверхности (для дерева по дереву μ=0.4) приложена горизонтальная сила F= 10 Н.

Чему равна Fтр ? Будет ли тело двигаться, и если да, равномерно или ускоренно? (Указание: сравните F и μ·P)

Cложение векторов

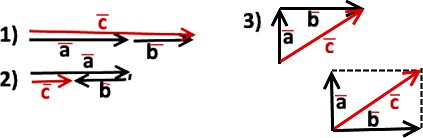Примеры сложения векторов приведены на рисунке:

𝒂⃗ + ⃗𝒃 = ⃗𝒄 . 1) и 2) – это метод «сложения шагов».

В 3) показано сложение векторов двумя способами: как

«сложение шагов» и «сложение методом параллелограмма»). Видно, что результат один и тот же

(красный вектор ⃗𝒄 ).

Разложение векторов и более сложный случай силы трения.

На двух рисунках изображен брусок на наклонной плоскости с двумя разными углами наклона α. Поставьте себя на место бруска. Случай a) – тело покоится.

Исходной является сила притяжения, вес P бруска. Вектор P мы, используя метод параллелограмма, разложили на 2 вектора:

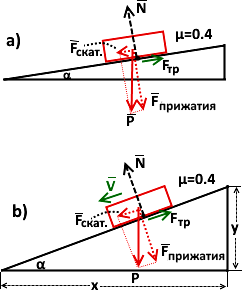1. силу прижатия к плоскости перпендикулярно плоскости: Fприжатия, 2)и силу скатывания продольно плоскости: Fскат.

Случай с малым наклоном α. Тело покоится. Сила прижатия бруска к плоскости здесь уже не вес бруска P, а его часть Fприжатия, перпендикулярная плоскости. Но он велика. А сила скатывания Fскат

–мала. Это случай силы трения покоя. Fскат. < μ·Fприжатия, тело покоится.

При увеличении наклона α Fприжатия, (как и μ·Fприжатия )

уменьшается. А вот сила скатывания Fскат. при этом увеличивается.

И при определенном наклоне имеем Fскат. > μ· Fприжатия, Брусок

начинает скользить по плоскости вниз.

Как мы позже узнаем, что увеличивая наклон α до момента начала скольжения бруска, легко найти значение μ. Для любой пары материалов. По отношению y и x: μ=y/x. Можете проверить это для пары дерево-дерево. Это простой способ определения μ.

Но можно найти μ и прямо, замеряя динамометром Fтр и считая μ= Fтр/P.

Замечание: Сила N на рисунках –это сила реакции плоскости на Fприжатия бруска.

Суммируем. Если приложить к телу на горизонтальной плоскости горизонтальную силу F, начиная с нуля, то сначала тело двигаться не будет, при этом Fтр = F по величине. Когда сила F достигает величины = μ·P тело начнет скользить. При дальнейшем увеличении F сила Fтр не меняется, Fтр = μ·P.

Если надо уменьшить силу трения, то используют смазки или подшипники. Если надо увеличить, то, например, на дорогах используют специальную резину на колесах или посыпают дорогу песком.

Давление

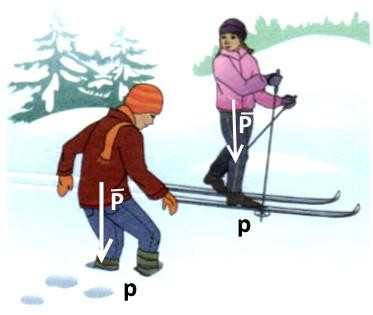Есть 2 разных понятия в физике, которые часто путают: сила давления P, и давление p. У девочек на рисунке сила давления примерно одинакова – это их вес P. Но у девочки на лыжах эта сила давления распределяется на большую площадь лыж S. Поэтому снег не продавливается. У девочки без лыж площадь обуви s невелика. Давление: p – это сила на единицу площади, p=F/S. У девочки на лыжах давление на снег p невелико, у второй – оно большое, снег не выдерживает, продавливается.

Правый рисунок показывает, как уменьшить давление p на лед. Левый рисунок показывает, как увеличить силу давления, чтобы лучше сжимать или даже резать (пассатижи, кусачки, щипцы, ножницы). Объясните.

Единица давления: (p=F/S), 1 Па (паскаль)=Н/м2 . Это очень мало.

Единица названа в честь Блеза Паскаля, (1623-1662) французского молодого гения, сделавшего 1-й калькулятор. Кроме всего прочего, он исследовал, как меняется атмосферное давление с высотой, при подъеме на гору.

Закон Паскаля

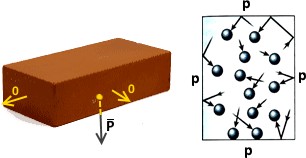
На левом рисунке показано, что давление твердых тел p, как и их вес P, направлены только вниз. В других направлениях давление p =0.

На правом рисунке показано давление в

газообразных и жидких телах. Оно производится ударами частиц. Во всех направлениях (на все стенки) p одинаковое. Это явление называется законом Паскаля.

История изучения давления

Однажды рабочие, копающие колодцы, обратились к Галилею с проблемой. Им не удавалось, откачивая насосом воздух в трубе сверху, поднять воду выше 10 метров от уровня воды. Имеется в виду уровень воды в колодце или в сосуде, откуда ее закачивали на верхние этажи зданий.

До тех пор считалось, что «природа не терпит пустоты» и поэтому можно с помощью насоса, откачивая воздух, поднять воду на любую высоту.

Галилей поручил разобраться с проблемой своему ученику

Торричелли. Оказалось, что механизм подъема воды совсем другой. Вода поднимается не из-за создаваемого разряжения сверху, а из-за давления воздушной атмосферы сверху вниз на саму поверхность воды, откуда ее качают. Воздух весом своей атмосферы выжимает воду вверх на 10 м, но не больше.

Торричелли также выяснил, что если заменить в сосуде воду ртутью, то насосом можно поднять ртуть только на 76 см, что в 13.6 раз меньше столба воды 10 м (точнее 9.8 м). Плотность ртути как раз в 13.6 раз больше чем у воды.

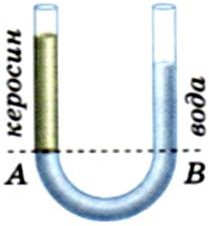Слева показана U-образная трубка с открытыми концами, заполненная слева керосином, а справа водой. Плотность керосина – 0.8 кг/дм3, плотность воды – 1 кг/дм3.

В трубке ниже линии AB вода в равновесии.

В коленах выше линии AB для равновесия вес керосина и вес воды

должны быть одинаковыми. Из-за разных плотностей высота столбика керосина должна быть выше столбика воды по соотношению 1/0.8 .

Давление определено как p=F/S, единица p в СИ 1 Па=Н/м2. В этих единицах атмосферное давление (1 атмосфера, 1 ат) = 100 000 Па. Почему такое большое неудобное число? Всё дело в большой единице площади 1 м2.

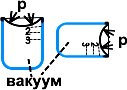
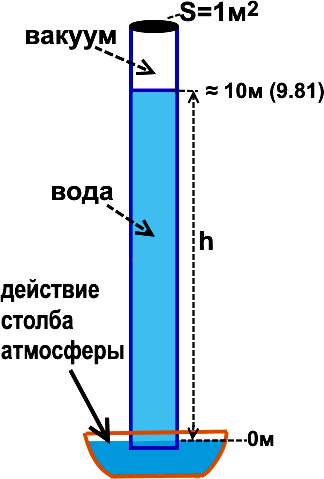Покажем это, исходя из того, что атмосфера уравновешивается столбом воды 10 м. Возьмем лощадь поперечного сечения S=1 м2, для наглядности и простоты вычислений. Верх трубы закрыт. Над водой в трубе вакуум,

т.е. давления сверху на столб воды нет.

Считаем. Объем столба воды V=S·h=1 м2 ·10 м =10 м3. Масса m=10 т. Вес, т.е. сила давления на условную площадь на уровне h=0 P=mg =

=10 000 кг ·10 м/c2 = 100 000 Н. Давление (F/S) p=P/S=100 000 Н/1 м2 = 100 000 Па. Ясно, что при такой единичной площади вес столба воды очень большой, вес массы 10 т. Давление атмосферы = 100 000 Па.

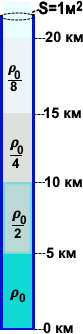
Теперь о давлении атмосферы. Мысленно представьте себе подобную же трубу с сечением 1 м2, но очень высокую, километров 50, для расчета силы давления всего столба воздуха. На уровне моря плотность воздуха в 1000 раз меньше плотности воды ≈1 кг/м3 (точнее 1 .3 кг/м3).

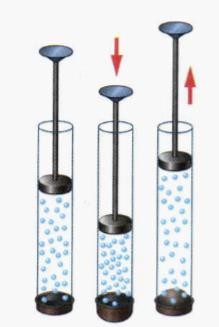
Но всё дело в том, что плотность воздуха уменьшается с высотой. В два раза каждые 5 км. Это потому, что как показано на правом рисунке воздух сжимается под давлением на него (в данном случае под давлением слоев воздуха, находящихся выше.

Сосчитаем приблизительно вес столба воздуха, как и в предыдущем примере. Вес нижнего фрагмента 𝝆0Vg ≈1кг/м3 ·(5000м·1м2)·10 = 50 000 Н. 2-й столб – 25 000. 50+25+12.5+6.2… В сумме получаем p ≈ 100 000 Н/1 м2. Как и водяного столба 10 м.

При подъеме в горы каждые 5 км давление постепенно уменьшается в 2 раза.

Первым изучил изменение давления атмосферы с увеличением высоты Паскаль.

Приборы для измерения давления

На рисунке слева показан самый простой прибор для измерения давления.

Это банка, закрытая упругой (резиновой) пленкой. Внутри банки вакуум, пленка прогибается под внешним давлением. Внутри есть шкала. На рисунке по этой шкале давление равно 1 атмосфере. Показание не зависит от положения банки.

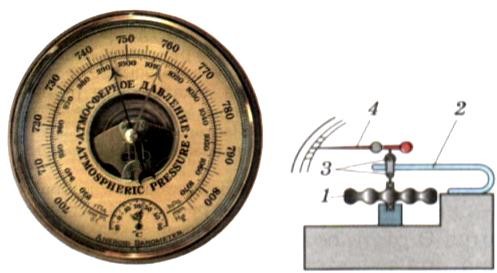Очень похож (слева) на предыдущий простой прибор и барометр («баро» – давление) для измерения текущего атмосферного давления. Это (1) – коробочка между двумя гофрированными (волнистыми) крышками. Из коробочки откачан воздух. Под внешним давлением атмосферы ее поверхность прогибается, стрелка прибора поворачивается.

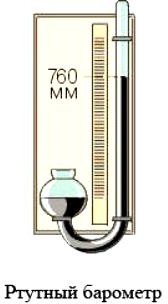
Справа показан ртутный барометр. Давление атмосферы может измеряться в

«миллиметрах ртутного столба». 760 мм – нормальное давление, если выше –

«повышенное давление».

Ниже 760 мм – «пониженное давление». Значительное отклонение давления от нормального вызывает недомогание у многих людей.

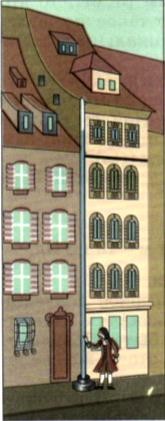
Справа изображен водяной барометр, сделанный Паскалем для наблюдения постоянных изменений атмосферного давления. Труба 11 м.

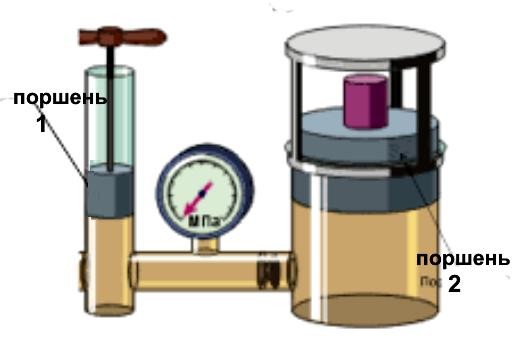
Прибор на рисунке слева – манометр – прибор для измерения давления газа и жидкости в промышленности.

(1)-это штуцер – место подключения. Основная часть (2)- это сплюснутая и изогнутая трубка, запаянная с другого конца. Под давлением трубка разворачивается и это передается на стрелку.

Показанный на рисунке манометр проградуирован в МПа

«мегапаскалях». Значение на приборе 0.1 МПа – это 100 000 Па, 1 ат.

Одна атмосфера соответствует 10 м водяного столба. Подводные лодки могут плавать на глубине 300 м. Это 30 атмосфер, 300 т веса на каждый м2 поверхности.

Батискафы имеют малые размеры и часто сферическую форму.

Поэтому могут опускаться до 500 м.

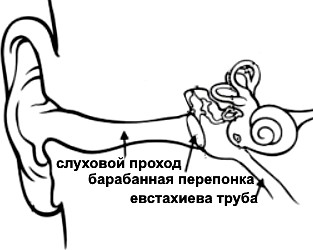
Если нырнуть на глубину 3 м, то начинают болеть барабанные перепонки из-за разного давление с двух сторон перепонки. Нужно сделать глотательное движение, чтобы давление за перепонкой в «евстахиевой трубе», соединенной с носоглоткой, выровнялось с внешним давлением.

То же самое происходит при взлете самолета. Только в этом случае давление снаружи меньше внутреннего.

При погружении с аквалангом давление на человека возрастает до нескольких атмосфер. Почему же легкие человека не сдавливаются? Потому что газ из баллонов подается в них под большим повышенным давлением.

Изменение давления с высотой

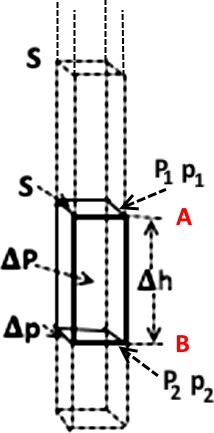Когда мы рассматривали давление столба атмосферы, мы выбирали для удобства S=1 м2, поскольку давление – это сила на единицу площади. Сейчас мы будем использовать объекты с сечением S, а потом полученный вес P делить на S.

Кроме того, при расчете давления атмосферы мы делили весь столб для удобства на части. Т.е. мы рассматривали вклад каждого фрагмента в вес P, а значит, и в давление p.

Найдите на рисунке точки A и B (красные). На уровне A полный вес – PА . Давление pА на уровне A создается этим весом (PА): pА= PА /S.

На уровне точки B общий вес столба выше точки B складывается из столба выше A и выделенного фрагмента между A и B высотой 𝚫h (символ 𝚫 читается

«дельта», означает «фрагмент», «часть»). Вес выше B увеличен на вес 𝚫P, а давление увеличилось в B на 𝚫p=𝚫P/S. 𝚫P = m·g = (𝝆·𝚫V)·g = 𝝆·(𝚫h·S)·g.

𝚫p=𝚫P/S= 𝝆·(𝚫h·S)·g/S. S сокращается, p не зависит от S: 𝚫p= 𝝆·𝚫h·g.

Мы получили простую и важную формулу увеличения давления при увеличении глубины 𝚫h: 𝚫p = 𝝆·𝚫h·g .

С какой силой вода, налитая в аквариум до высоты h давит на боковое стекло и

дно аквариума? Площадь S – часть площади бокового стекла, смачиваемая водой.

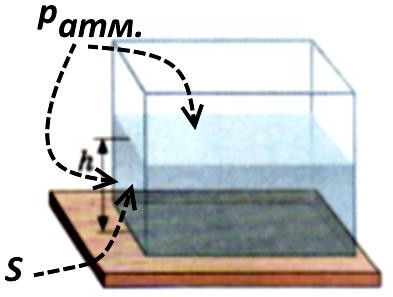Давление атмосферы Pаmм давит на боковое стекло с двух сторон, изнутри и снаружи. Поэтому его учитывать не надо.
С глубиной h давление воды p меняется от 0 до 𝝆gh, 𝝆воды=1000 кг/м3.
Среднее давление воды: pср=(0+ 𝝆gh)/2= 𝝆gh/2.
Сила давления воды на боковое стекло: F= pср·Sбок= 𝝆gh/2· Sбок Если, к примеру, h=0.4 м, Sбок=0.4·0.5=0.2 м2, то

F бок= 𝝆gh/2·Sбок=( 1000·10·0.4/2 ·0.2 ) Н= 400 Н (вес массы 40 кг !).

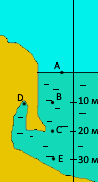
Давление воды на дно: pдна= 𝝆gh =1000·10·0.4=4000 Па. Или в атмосферах: 1 ат.·( 0.4м/10м) =0.04 ат.

Вопрос. Какое давление в разных точках под водой и в пещере (в ат.)?

Архимед. Родился в Сиракузах, греческой колонии на острове

Сицилия. Обучался в Египте, затем вернулся в Сиракузы.

Об Архимеде известно много легенд. По одной, Архимед проверял неподдельность золотой короны царя. Он понял смысл силы выталкивания предметов, погруженной в жидкость (Закон Архимеда).

По 2-й легенде, он, используя принцип рычага, смог спустить на воду большой корабль. По 3-й легенде, смог поджечь вражеские корабли, на которые воины вместе направили лучи солнца, отражая их и направляя блестящими щитами на корабли

По легенде, был убит солдатом. Солдат приказал ему следовать за ним. Но Архимед отказался идти. Закончить решение задачи показалось ему важнее.

Сила выталкивания Архимеда

На тело, погруженное в жидкость, действует сила выталкивания (вверх), равная весу вытесняемой телом жидкости (Закон Архимеда).

По преданию, поняв эту истину, сидя в ванной, Архимед выскочил из нее с криком «Эврика» («Нашел»). Доказательство его было таково:

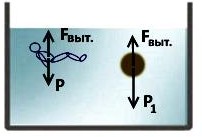Плотность у человеческого тела примерно такая же, как и у воды. Тело плавает в равновесии, полностью погруженное в воду. Значит, силу веса тела P уравновешивает некая сила Fвыт., противоположная и равная силе P.

Если в воду погрузить тело с тем же объемом, но большей плотности, чем у воды, то сила выталкивания Fвыт. останется прежней

(она определяется только объемом тела и равна весу вытесненной им воды). В этом случае вес тела P больше Fвыт., тело тонет. Если 𝝆тела < 𝝆воды, то тело всплывает вверх.

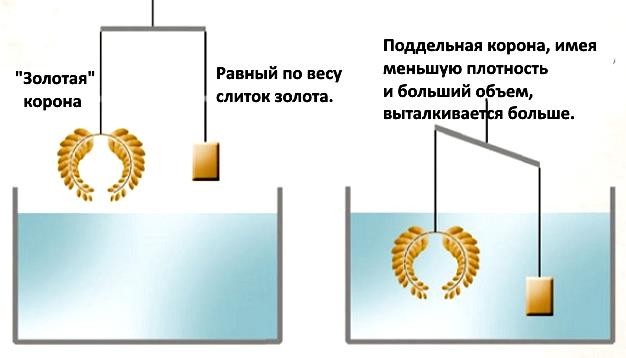Однажды царь поручил Архимеду проверить

«неподдельность» его золотой короны. Вот как поступил Архимед: Если корона поддельная, то к золоту добавлено серебро. Плотность золота ≈20 г/см3, у серебра ≈10 г/см3. Удельная плотность короны станет меньше, чем у золота.

А при одинаковом весе объем короны будет больше, чем у слитка. Выталкивающая сила у короны будет больше. Равновесие весов нарушится. Это и случилось.

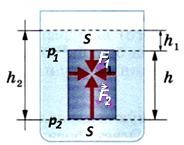Теперь обсудим как возникает силы выталкивания

Силы с боков на погруженный в воду предмет мы не рассматриваем, т.к. они уравновешивают друг друга. Площади сверху и снизу равны S.

Выше мы разобрали, что сила p2 больше p1 по величине на 𝝆gh. Значит, разница сил F2 – F1 = p2·S – p1·S =(p2 – p1)S = 𝝆gh·S = 𝝆g(h·S)

=g𝝆V.

g𝝆V – это вес вытесненной предметом воды (жидкости в общем случае). Замечание: Если предмет плотно прижат ко дну (вода не подтекает), то F2=0! Сила F1 прижимает тело ко дну.

Плаванье тел на поверхности

Доска толщиной h плавает в воде. 𝝆д дерева 0.8 кг/дм3. На какую часть x от высоты h доска погружена в воду?

Решение. Примем, что площадь доски S, объем V=Sh, масса m=𝝆д·Sh. Пусть доска погрузится на часть x своей высоты h. Сила Архимеда уравновешивает вес: Pв = Pд. Вес вытесненной воды Pв = 𝝆в·V·g = 𝝆в·(S(xh))·g . А вес доски Pд= 𝝆д· (S·h)·g . Приравниваем:

𝝆в·(S(xh)) ·g = 𝝆д·(S·h) ·g

S, g, h справа и слева сокращаются: 𝝆в·x = 𝝆д .

Получили: x = 𝝆д /𝝆в 𝝆д =0.8, 𝝆в· = 1. Откуда x=0.8

Картинки по запросу ватерлиния (в воде x совпадает с 𝝆 предмета). Это можно использовать: Справа показан плавающий в океане айсберг. 𝝆 льда = 0.9 кг/дм3.

Плаванье судов

Почему корабль держится на плаву? Потому что вес вытесненной воды в определенном положении равен весу корабля вместе с грузом.

На кораблях всегда отмечен уровень максимально допустимого

погружения корабля. Эта линия называется ватерлинией.

Воздухоплавание, аэростаты

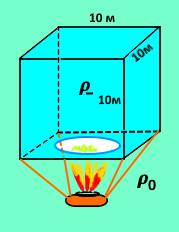
Предположим, аэростат имеет оболочку с объемом V=10м х10м х10м =1000 м3.

Оболочка открыта снизу, там идет подогрев воздуха внутри оболочки. Снаружи воздух с нормальной плотностью 𝝆0=1.3 кг/м3.

Внутри воздух из-за подогрева горелкой имеет плотность 𝝆_ =1.0 кг/м3.

Какой вес может поднять аэростат? Вес оболочки и нагревателя с корзиной не учитывать (мы их включим в поднимаемый шаром вес).

Решение. Считаем силу выталкивания, т.е. вес вытесненного аэростатом «холодного» воздуха: Fвыт=(𝝆0V)g=(1.3·1000)10=13 000 Н.

Считаем вес внутреннего воздуха:

P1=(𝝆·V)g=(1.0·1000)10=10 000 Н.

Подъёмная сила F= Fвыт – P1=(13000-10000) H =3000 Н.

Ответ: Подъёмная сила 3000 Н. Это вес массы 300 кг. (сюда мы включили также вес оболочки с корзиной и нагревателем).

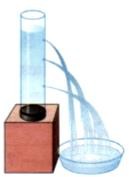Интересные опыты

(Слева). Из дырочек на разном уровне цилиндрического сосуда вода выходит с разным напором. Этот опыт показывает, что с глубиной давление в жидкости возрастает.

(Справа). Налейте в цилиндрический стакан воды. Закройте сверху плотно листом бумаги. Медленно, придерживая лист рукой переверните стакан. Уберите руку. Лист не отделяется от стакана. Объясните. Ответьте, какой высоты может быть стакан в опыте?

Магдебургские полушария

В 1854 г бургомистр города Магдебурга Отто Герике устроил опыт для доказательства давления атмосферы воздуха и его силы. Бралось 2 половинки сферы. Их соединяли и откачивали воздух. В первом опыте обе половинки с треском смялись, не выдержали давления.

Считем. Возьмем площадь сечения между полусферами 1 м2. Как мы помним на единичную поверхность атмосфера давит как

метровый столб воды (весом массы 10 т).

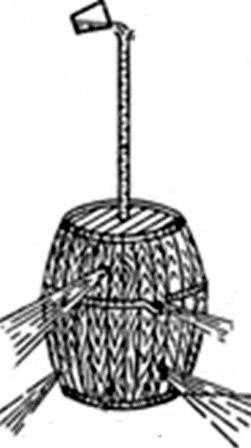
Опыт Паскаля с бочкой. По просьбе Паскаля крепкую дубовую бочку до краев наполнили водой и наглухо закрыли крышкой. В небольшое отверстие в крышке заделали конец вертикальной стеклянной трубки такой длины, что конец ее оказался на уровне второго этажа. Не успел Паскаль вылить в нее и несколько стаканов, как вдруг, к изумлению обступивших бочку зевак, бочка с треском лопнула.

Гидравлический пресс

Опыт с бочкой показывает, что с помощью тонкого цилиндпра (или трубки) можно небольшим количеством

воды (или изменением объема в тонком цилиндре) получать очень большие силы. В технике мощные прессы используются часто. Например, для штамповки деталей из металлических листов-заготовок.

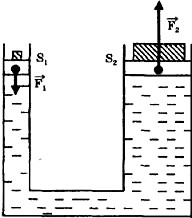
Обсудим принцип действия (слева). Двигая вниз поршень в узком цилиндре, можно увеличивать давление в жидкости. Сил для этого много не надо, так как S1 мало: F1= p·S1.

Поскольку давление в обоих цилиндрах p одно и то же, а S1 во много раз больше, то F2= p·S2. оказывается очень большим.

Гидравлический домкрат для автомобиля работает на этом же принципе.

Водяная колонка – поршневой жидкостный насос

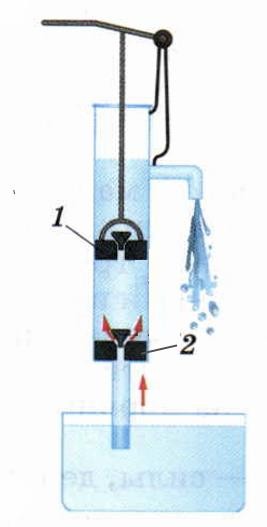
Рассмотрим при каких движениях рукоятки открываются и закрываются клапаны в поршнях 1 и 2. При движении поршня 1 вверх его клапан закрывается, вода льется из трубы. В это время клапан цилиндра 2 открывается и вода затекает снизу в область между поршнями.

При движении поршня 1 вниз все идет наоборот.

Отбойный молоток

Воздух под большим давлением, полученным в компрессоре, через гибкий шланг подается в молоток. Переключатель попеременно изменяет подачу воздуха то по одну сторону поршня, то по другую. С большой частотой. Это слышно по звуку при работе.

Поршень ударяет по копью молота. Работа и мощность. Энергия

Мы обращаемся к новым понятиям: «работа» и «энергия». Эти понятия в физике не совпадают с этими же понятиями в нашем быту. Будьте внимательны к их точным определениям в физике. Мы увидим дальше общность в понятиях работа и энергия.

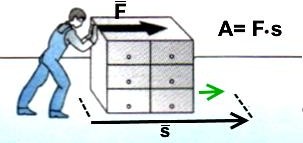
Точное определение понятия «работа». Смотрите на картинку: человек толкает груз. Так вот, если он передвинет груз на дистанцию s, прикладывая для этого силу F в направлении движения, то выполненная работа A равна: A=F·L.

1. Если прикладывается сила, но тело не движется, то работа в смысле физики не производится. Даже если тратится много биологической энергии. F·0=0.
2. Если при перемещении тела сила не применяется – это не может считаться работой в смысле физики. Т.к. A=F·L = 0·L=0.

Единица измерения работы 1 джоуль (1 Дж) = 1Н·1м. Используется и килоджоуль (кДж). Джоулем эта единица названа в честь английского физика Джеймса Джоуля (1818-1889), обосновавшего на опытах закон сохранения энергии.

Оказалось, что понятие «работа» входит составной частью в более общее понятие «энергия». Энергия проявляется в очень многих своих видах и сохраняется при переходе из одного вида в другой. Энергия водопада преобразуется в электрическую энергию, электрическая энергия переходит в тепловую, и т.д.

Рассмотрим процессы:

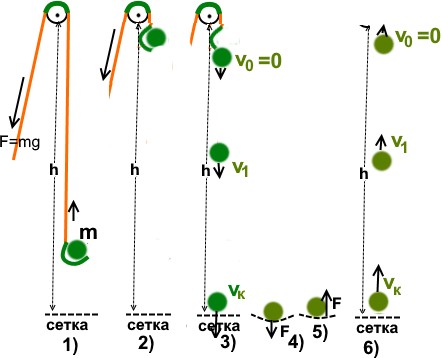- 1. Шарик массой m посредством блока поднимается на высоту h. Прикладывается сила F=P=mg на шарик вверх. При этом тянущий выполняет работу A=F·h=m·g·h.
  2. Поднятый на высоту h, шарик отпускается и начинает падать на упругую сетку.
  3. В начальный момент падения скорость шарика v0=0. По мере падения его скорость увеличивается с ускорением g. Здесь работу выполняет сила притяжения: A=F·h=m·g·h. Результатом работы будет конечная скорость шарика vк. (Кинетическая энергия имеет вид mv2/2.)
  4. Шарик выполняет работу над сеткой, прогибая ее с некоторой силой F на некоторый небольшой интервал 𝚫h. Его работа A=F·𝚫h. Шарик при этом полностью теряет скорость.
  5. Теперь упругая сетка выполняет работу над шариком, прилагая силу F, но направленную вверх на дистанции 𝚫h: A=F·𝚫h. Шарик восстанавливает свою прежнюю скорость vк , но направленную вверх.
  6. Внимание! Здесь есть сложность. Шарик за счет скорости vк поднимается вверх и, преодолевая силу притяжения, теряет скорость. Но! Перемещение v направлено против силы F. Трактуют это так, что в этом случае F·h отрицательно. Как это понять? Надо аннулировать результат работы падения 3), вычесть его. Значит, шарик должен подняться на высоту h, а скорость шарика v должна упасть до 0.

Но, как увидите чуть ниже, проще всё это объяснять в терминах энергии.

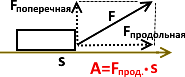Важно еще отметить, что работу совершает только продольная к s часть силы F. Если сила F отличается по направлению от S, надо разложить F и использовать только продольную составляющую F: A=Fпрод·s.

Энергия

Вы заметили, что при рассмотрении шарика выше на всех этапах проявлялась одна и та же величина работы. Понятие «энергия» является однотипным с понятием

«работа», но более широким. Измеряется энергия, как и работа, в джоулях. Но у нее есть много больше видов, чем просто механическая работа A=Fs. Есть

электрическая энергия, и тепловая, и атомная и т.д. Энергия переходит из одного вида в другой.

Рассмотрим прежнюю картину с шариком в терминах «энергий».

- - 1. Шарик поднимают вверх, при этом он получает

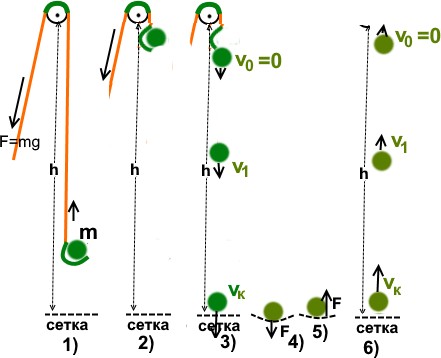«потенциальную энергию» Eпот=mgh. «Потенциальная» – это способность совершить работу в будущем. Т.е. это запас энергии, который можно реализовать в работе.

2,3)Шарик падает вниз, его потенциальная энергия переходит в энергию движения – «кинетическую энергию» Eкин=mv2/2. По пути Eпот уменьшается, и настолько же увеличивается Eкин.

4,5)Кинетическая энергия Eкин полностью переходит в упругую энергию сетки Eу, которая, затем снова из энергии

упругости сетки переходит в кинетическую энергию Eкин шарика.

6)Кинетическая энергия mv2/2 возвращается в потенциальную энергию

Eпот=mgh.

И понятно, что энергия измеряется в тех же единицах (джоуль) что и работа.

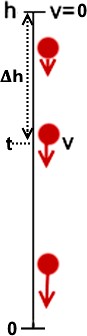Потенциальная энергия уменьшается, а кинетическая энергия увеличивается.

Предположим, что тело начинает падать с какой-нибудь высоты h. К моменту t тело пролетело дистанцию, которую обозначим 𝚫h, и приобрело скорость v.

Его потенциальная энергия Eпот=mgh уменьшается по мере увеличения 𝚫h на

𝚫Eпот=mg ·𝚫h, а кинетическая энергия увеличивается от 0 до Eкин=mv2/2.

Выведем всё это из закона равноускоренного движения с ускорением g.

Запоминать вывод не надо, посмотрите только логику вывода.

Сначала вспомним, как высота падение зависит от скорости v в конце 𝚫h:

𝚫h=vср·t=(v/2)·(v/g)=v2/(2g), т.е. 𝚫h=v2/(2g).

Умножим обе части на силу F=mg: 𝚫h(mg)=v2/(2g) ·(mg). Справа g сокращается. Получаем mg·𝚫h=mv2/2.

Слева – уменьшение 𝚫Eпот=mg·𝚫h, справа значение Eкин=mv2/2.

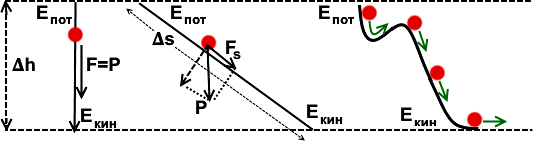Рассмотрим движение вниз по наклонной плоскости. Путь 𝚫s увеличился по сравнению с

𝚫h. Но сила вдоль пути FS уменьшилась во столько же раз (мы разложили силу P на 2 составляющие).

Таким образом, значения F·𝚫h и FS·𝚫s одинаковы.

Каждый небольшой участок кривой траектории – это наклонная плоскость. Поэтому независимо от вида траектории спуска сверху Eпот=P·𝚫h. А внизу Eкин= mv2/2= P·𝚫h . Во всех 3 случаях v внизу одинаково, хотя ее направление внизу разное.

Мощность

Часто возникает вопрос не о величине работы, а о том, с какой скоростью происходит ее выполнение. Т.е. считается работа, производимая в единицу времени. Эта величина носит название мощности. Обозначается W=A/t. Единица мощности называется ватт (Вт).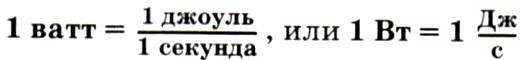

Используются и единицы «киловатт» кВт=1000 Вт (часто в быту). и «мегаватт» мВт=1 000 000 Вт (в промышленности).

Шотландский инженер, изобретатель Джеймс Уатт (1736-1819).

Изобретатель универсальной паровой машины. Работы Уатта положили начало промышленной революции вначале в Англии, а затем и во всем мире.

В свое время предложил единицу мощности «лошадиная сила»

1 л.с.=735 Вт, несколько меньше 1 кВт. Она используется и сейчас для определения мощности двигателей автомобилей. Единицы 1 кВт и 1 л.с. примерно равны мощности электроплитки.

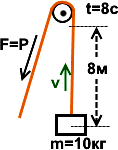Задача. Человек посредством блока поднимает груз массой

m=10 кг на высоту h=8 м за время t=16 с. Найти мощность процесса W? Решение. Выполняется работа по подъему A=F·h=(mg)h=100·8=800 Дж.

W=A/t=(mg)h/t = 800 Дж/16 c=50 Вт.

Рассмотрим другой подход: W=A/t=(mg)h/t =(mg)(h/t)=F·v. v=8м/16с =0.5 м/c

W=(mg)·v=(100 Н)·(0.5 м/c) =50 Вт.

Мы получили 2-ю важную формулу для W: 1)

W=A/t

Гидростанция

, 2) W=F·v.

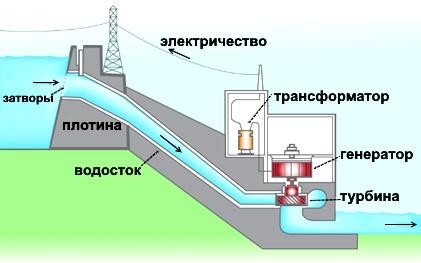Задача. Есть плотина с гидростанцией. Плотина нужна, чтобы поднять уровень воды в водохранилище повыше. За время t=1 мин. протекает V=500 м3 воды. Высота между входом в водосток и турбиной h=6 м. Вычислить мощность W, выделяемой водой на турбине.

Решение. 1)Вычислим изменение потенциальной энергии указанного объема воды Eпот. (или, что то же, работу, производимую силовым полем Земли A при спуске воды до

турбины за указанное время).

Eпот.=mgh=(V·𝝆)gh=(500 м3·1000 кг/м3)·10 м/с2·6 м = 500 000 · 10 · 6 Дж=30 000 000 Дж.

W=Eпот./t =30 000 000 Дж/60 c=500 000 Вт.

Понятие КПД

В предыдущей задаче

воды превращается в

воды, затем во

вращательную энергию турбины. На генераторе она превращается в

Eпот

Eкин

электрическую энергии. Далее на трансформаторе электроэнергия преобразуется в электроэнергию же, но с высоким напряжением, чтобы с меньшими потерями ее передать на дальние расстояния.

Но часть энергии в этих процессах теряется. Допустим, теряется 30% энергии воды. 70% передается дальше. Вот эти 70% и называются КПД (коэффициентом полезного действия).

В предыдущей задаче дальше передается мощность 500 000·0.7=350 000 Вт.

Ветряные двигатели

Аналогично описанной выше электростанции действуют и ветряные двигатели. В них кинетическая энергия воздуха (ветер) преобразуется в энергию вращения ротора генератора и далее электроэнергия по проводам передается вниз. Мощность небольших «ветряков» в личном хозяйстве порядка 2-5 кВт.

Простые механизмы: рычаги, наклонная плоскость, блок

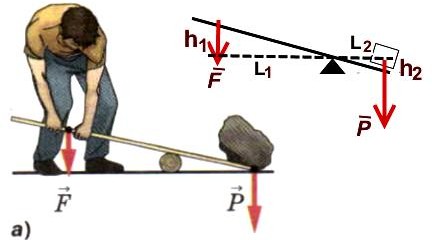Вариант рычага а). Точка опоры внутри рычага.

Левый конец опускается вниз на h1. Правый поднимется на h2. Выполняемую работу можно определить как F·h1. Но можно ее определить и как P·h2. Это одна и та же работа: F·h1= P·h2. То, что обозначено как L1 и L2 – называется «плечо». По рисунку видно, что плечо L1 больше плеча L2 в 2 раза. Откуда следует, что h1

больше h2 в 2 раза. А из равенства F·h1= P·h2 следует, что F в 2 раза меньше P. Такой рычаг позволяет снизить усилия соотношением плеч. Правило:

силы на рычаге находятся в обратной пропорции к плечам.

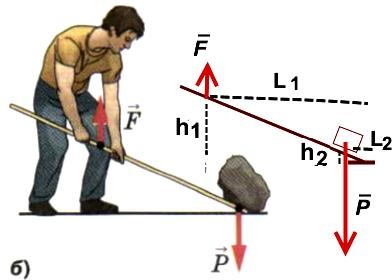Вариант рычага б). Точка опоры на самом конце рычага

h1 и h2 оба направлены вверх. h1 и h2 пропорциональны L1 и L2

, которые надо отсчитывать от крайней справа точки (точки упора). Здесь соотношение плеч порядка 6. Из соотношения F·h1= P·h2 следует, что F в 6 раза меньше веса P.

Использование наклонной плоскости

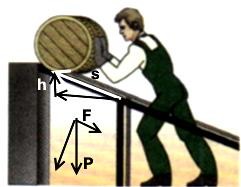
На рисунке рабочий вместо того, чтобы поднимать бочку на высоту h, вкатывает ее по наклонной плоскости длиной s. h и s указаны условно, хотя их соотношение отражено. Силу веса P мы разложили на 2 составляющие. F направлена вдоль плоскости. Как и в предыдущих случаях

работу можно представить, как P·h, так и как F·s. По соотношению векторов видно, что сила F во столько раз меньше силы P, во сколько раз s больше h,

Выигрыш в силе F по сравнению с P равен проигрышу в длине пути s по сравнению с высотой h.

Блок

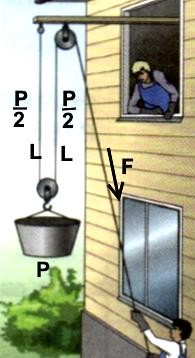
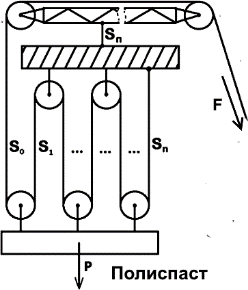Если подъем не производится, то вес груза P распределяется по двум канатам по P/2. Значит человек, держащий груз должен прилагать силу P/2. Также видно, что, чтобы поднять груз на высоту L, человеку нужно выбрать трос длиной 2L. Лишний раз подтверждается равенство работ P·L= P/2 ·2L .

Справа показано устройство типа блока, которое позволяет снизить силу в 6 раз. Но длина выбираемого троса увеличивается в 6 раз.

Этот вид блока называется «полиспаст».

Применение рычага в быту

На этих весах используется принцип рычага. Можно взвешивать тяжелые вещи.

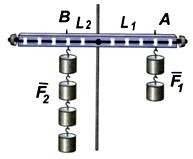Рычаг с осью вращения. Равновесное положение системы

Это случай рычага с центром вращения внутри рычага. Отношение плеч L1/L2=2. Задайте себе вопрос: «Какую силу F1 надо приложить в т. A, чтобы удерживать в равновесии силу F2 в т. B?». Конечно, в 2 раза меньше F2 ! В обратной пропорции плеч L1 : L2.

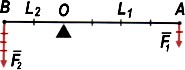Обратите внимание, как правильно оформлять схематически предыдущий вариант рычага.

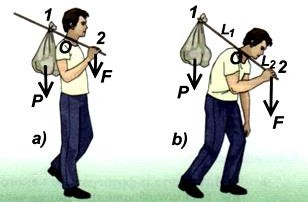Задача. На двух рисунках изображен юноша, несущий груз P. Точка O – точка опоры рычага на плече.

F –усилие руки, направленное вниз. L1 и L2 – плечи сил P и F. В случае a) L1 : L2 =1 :2. В случае b) L1 : L2 =2 :1.

Для a) и b) выразите силу F через P по соотношению плеч. 2.Сложив P и F, найдите общую нагрузку в точке O. Сравните.

Момент силы

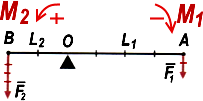Рассмотрим новое и очень важное понятие: момент силы. Это способность конкретной силы поворачивать систему вокруг некого центра O. Эта способность зависит и от самой силы, и от ее плеча L: M=F·L

В математике и физике «положительным» считается поворот против часовой стрелки. Например, сила F1 разворачивает систему вокруг O по часовой стрелке, поэтому ее момент берется со знаком «-». У M2 знак «+».

Сосчитаем сумму моментов сил с учетом знаков: M1+M2 = – F1·L1 + F2·L2 .

Поскольку в данном случае F1·L1= F2·L2 , то с учетом знаков: M1+M2=0.

В физике это равенство 0 – обязательное условие равновесия системы.

Единица момента сил называется «ньютон-метр» (Н·м).

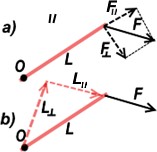В предыдущем примере силы F были перпендикулярны их плечам L. Если это не так, то нужно разложить либо F, либо L на поперечную () и продольную (II) составляющие по варианту a), либо по варианту b).

F раскладываем на продольную F и поперечную F к L . F II не работает на поворот! M=F·L . В данном случае L- это плечо силы F.
Нужно разложить L на Lи L к F, и использовать только L .

M=F· L. L- это плечо силы F.

Оба варианта дают одинаковые значения M!

Центр тяжести

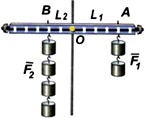
В рассмотренном варианте точка O была выбрана так, что моменты M1 и M2 уравновешивают друг друга. Такая точка O называется «центром тяжести» этой системы.

Ниже изображено тело с таким же центром тяжести. Подвешенное на нитку в точке O тело будет в равновесии. Хотя оно может свободно поворачиваться (в вертикальной плоскости и горизонтальной).

тела.

Центр тяжести плоской фигуры

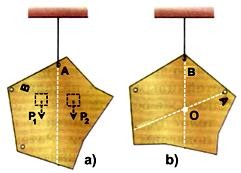Ищем центр тяжести плоского тела.

Подвешиваем его на нитке за точку A. Проводим линию на фигуре продольно к нити (белый пунктир). На рисунке отмечено 2 маленьких квадрата. Они просто демонстрируют, что разные части этого тела действуют так же, как массы на подвешенном рычаге с массами относительно точки вращения.
Подвешиваем это же тело за точку B. И тоже проводим линию. Две линии пересекаются в точке O. Это центр тяжести всего

Если попробовать подвесить тело еще за другую крайнюю точку, то

вертикальная линия обязательно пройдет через найденную точку O.

Эта точка очень важная. Вспомните, например, когда мы отражали силу тяжести вектором 𝐏⃗ , то начало вектора силы веса мы привязывали к центру тяжести.

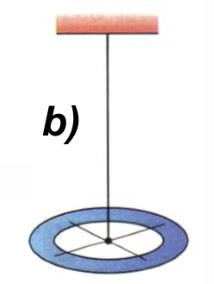Если тело бросить и оно при этом вращается, то вращение в полете будет происходить вокруг точка центра тяжести.

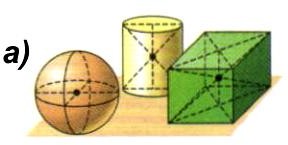Примеры положения центра тяжести в симметричных

телах.

Справа показано, что центр тяжести может находиться и вне тела.

Устойчивость

На рисунке показана линейка, с центром тяжести C в середине линейки. И есть центр вращения (свободного) в т. O (спица).

Рассмотрим 3 случая: a) т. O сверху, b) т. O снизу, c) т. O в центре.

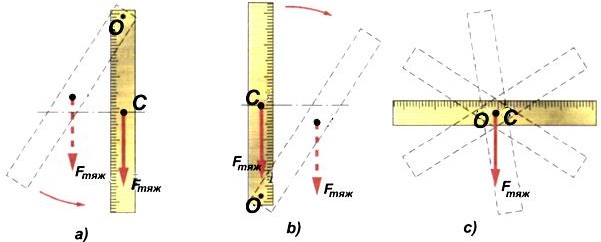С точки зрения рассмотренного рычага все случаи равновесные. Но.

1. равновесие устойчивое, линейка

качается около нижнего положения.

1. равновесие неустойчивое. Чуть сдвинутая вбок, линейка «опрокидывается» и переходит в устойчивое равновесие a).
2. положение безразличного равновесия. Линейка может свободно вращаться на оси, не выходя из равновесия. Примером могут быть колеса автомобилей. Отметьте, что положение устойчиво, если центр тяжести C ниже точки вращения O.

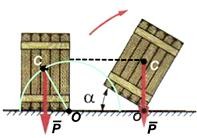Равновесие тел, имеющих площадь опоры

Площадь опоры ящика (слева) – это нижняя сторона ящика в исходном положении.

Если начать опрокидывать ящик, то до некоторого положения

ящика (угла α) это не получится. Далее он сам начнет опрокидываться.

В правом изображении ящика его центр тяжести (и симметрии) C

находится как раз над точкой O – осью вращения. Это вариант неустойчивого равновесия из предыдущего пункта. Из этого положения ящик либо возвращается в исходное положение, либо опрокидывается на бок.

Но отметьте, что центр тяжести C, двигаясь по окружности вокруг оси O (левый рисунок), сначала приподнимается до тех пор, пока точка C не окажется над точкой O. И только потом центр тяжести C начинает опускаться вниз, ящик опрокидывается.

Другой подход к проблеме устойчивости

В случае с линейкой мы подходили к устойчивости с точки зрения моментов сил. Сейчас мы разберем проблему устойчивости с точки зрения потенциальной энергии.

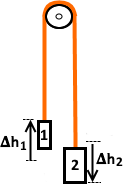Мы понимаем, что, когда есть возможность, тело снижает свое положение, уменьшая этим свою потенциальную энергию.

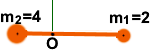
На рисунке показан блок с двумя массами, m1=1 и m2=2 (m1 < m2).

Понятно, что масса m2 перетягивает массу m1. Смещение 𝚫h1 вверх = 𝚫h2 вниз. Увеличение потенциальной энергии m1: 𝚫Eпот1= m1g 𝚫h1,

уменьшение потенциальной энергии m2: 𝚫Eпот2= – m2g 𝚫h2.

Ясно, что для всей системы 𝚫Eпот1 + 𝚫Eпот2= m1g 𝚫h1 – m2g 𝚫h2 <0.

Суммарная потенциальная энергия системы уменьшается.

Т.е. система ведет себя так, чтобы обшая потенциальная энергия системы уменьшалась (если это возможно).

Обратите внимание, что центр тяжести двух масс в нашем случае должен находиться ближе к m2. И сдвигается он в сторону смещения большей массы – m2.

Т.е. с опусканием массы 2 общий центр тяжести опускается.

Вообще, здесь корректно и удобнее использовать не центр тяжести, а близкое к нему понятие центра масс. Позже мы научимся его вычислять. Оказывается, изменение потенциальной энергии тела можно определять по изменению высоты центра масс.

𝚫Eпот= M·g·𝚫hц, где M – общая масса тела (в данном случае M= m2+m2), а 𝚫hц – смещение центра масс.

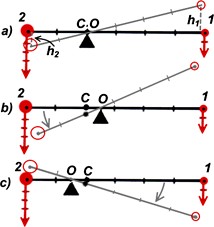Рассмотрим случай, когда тело состоит из 2 масс с центром вращения между ними.

Если одна масса опускается, уменьшая Eпот, то другая поднимается, увеличивая свою Eпот. Важно, уменьшится или увеличивается их общая Eпот = Eпот1+Eпот2.

Рассмотрим случай a), когда центр тяжести совпадает с центром вращения. Поскольку P1h1=P2h2, то при повороте нет изменения Eпот1+Eпот2. На сколько уменьшится Eпот2 (P2h2), на столько же увеличится Eпот1 (P1h1). Общая Eпот не меняется. Это условие безразличного равновесия.

b) и c) Центр масс смещен от центра вращения. При этом тело поворачивается, уменьшая свою общую потенциальную энергию.

Видим, что общее уменьшение Eпот системы совпадает с понижением ее центра масс. Если мысленно вес тела P поместить в центр масс, то очевидно снижение Eпот всего тела.

Конец учебника