Комплексные числа то вводили в программу средней школы, осознавая
их важность в современной жизни, то убирали, ссылаясь на то, что ученики воспринимают тему как излишне абстрактную, малопонятную, оторванную от жизни. Сейчас комплексные числа даются только на факультативах и в школах с математическим уклоном.
Я сторонник того, чтобы вернуть их в программу средней школы. Предлагается вариант объяснить их просто, чтобы всё было понятно, без излишней формализации, и показать их важность. Весь материал разбит на 7 уроков – 10 страниц.
Итак, комплексные числа.
Они появились, когда математикам понадобилось не отбрасывать решения квадратного уравнения с детерминантом <0 (типа x1,2=2±√(-9) )= 2±3√(-1) ), а работать с ними дальше. На это у них были свои причины. Далее числа этого типа были названы комплексными, т.к. они состоят из двух компонент. Комплексные числа оказались очень удобным средством во многих областях. Сферу их применения постепенно расширяли известные математики.
Проблема в том, что при развитии аппарата комплексных чисел математики использовали понятия и средства, уже разработанные прежде. Например, декартову систему координат, полярную систему координат, векторы, тригонометрию. Но при этом для комплексных чисел они часто вводили свою терминологию.
Вам следует понять некую условность и неоднозначность в организации терминологии. В качестве курьезного примера. В некоторых «научных школах» у нас произносят кОмплексные. В других – при таком произношении на вас посмотрят, как на плохо образованного. Потому что там принято произносить комплЕксные. В русских словарях стоит кОмплЕксные, попробуйте такое произнести. А в англоязычной Википедии об ударении даже не упоминается.
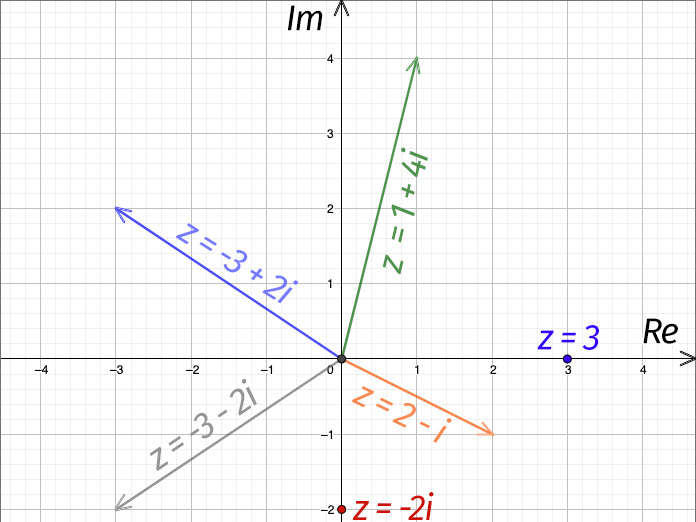
Обозначаются комплексные числа традиционно переменной «z», они имеют структуру типа z=2+3i, т.е. действительную и мнимую компоненты.
Пару слов о «мнимой единице i ».
Сначала ее определили, как i=√(-1). Потом, чтобы избежать знака «-» под корнем, i положили определять условием i2= -1. Но обходится молчанием, что при этом и i, и –i становятся фактически одним объектом, так как оба удовлетворяют условию i2 = -1. А в электротехнике вместо символа «i» стали использовать символ «j», чтобы не путать с символом обозначения тока i. Хотя буква j тоже используется в физике, для обозначения плотности тока.
В терминологии для этих чисел много того, что «принято», «предписано». Мы обсудим это всё по минимуму, так как наша тема определена, как «Введение».
Если вам говорят, что мнимое число – это нечто такое, что невозможно в принципе понять и представить, так же, как 4-е измерение, то не верьте, вас вводят в заблуждение! Вспомним натуральные числа, о том, что их используют и для «нумерации», и для определения «количества». Совсем разные понятия:
«3 объекта» и «3-й объект». В этом случае просто в разных ситуациях используют некое одно и то же множество объектов (натуральные числа) с их определенным набором операций, которых достаточно и для первого понятия, и для второго.
То же самое и с комплексными числами.
Для математиков – это множество объектов, для которых не возникает противоречий в операциях сложения-вычитания, умножения-деления, возведения в степень-извлечения корня. Тогда как для других множеств чисел это не так. Например, операция вычитания на множестве натуральных чисел может приводить к отрицательным числам, т.е. объектам уже другого множества.
Для физиков комплексные числа – это возможность смотреть на колебания, т.е. на гармонические функции типа cos(ɷt) и sin(ɷt), как на проекции на оси x и y движения по кругу. На круге проще рассматривать взаимные отставания и опережения колебаний «по фазе». Горизонтальная ось на рисунке обозначена Re (от real, действительный), вертикальная – как Im (от imaginary, мнимый).
Геометры же на плоскость комплексных чисел смотрят, как на обычную плоскость. Без различия действительной и мнимой компоненты. Просто на плоскости комплексных чисел удобно производить «угловые повороты» траекторий.
Таким образом, комплексные числа – это математическое множество объектов, которые своими свойствами облегчают кому-то рассмотрение каких-то явлений в своих областях. И всё!
В статье используются новые подходы:
- по-новому объясняется сложение аргументов комплексных чисел при их умножении;
- объясняется вывод формулы Эйлера, показан ее смысл;
- демонстрируется применение комплексных чисел в физике (тема «Резонанс»), это целесообразно использовать на уроках физики.
Это был ознакомительный фрагмент статьи.